This web page will instruct you on how to obtain the findings of 2875 tropical lines (when counting with multiplicity) that was used in the article "Tropically Constructed Lagrangians in Mirror Quintic Threefolds" where Lagrangians in the mirror quintic were constructed from tropical lines in the base of the torus fibration of the quintic. For the mathematical understanding of purpose and context, etc, I assume at this point basic familiarity with the article. The following is a merely algorithmic description in a "do it yourself" fashion. No mathematical understanding will be required for running the code below. If you don't want to go through the search of the lines but only want to inspect and play with the specific findings that Cheuk Yu and I used in the research article, jump to the last section of this webpage. The end result of the instructions on this webpage will be a rotatable plot of the tropical lines that were found, a snapshot of which is going to look as follows:

I chose the computer algebra package GAP for its ability to perform operations on integer matrices. In order to reproduce the findings of tropical lines, please install GAP on your computer and then put the following text files in your working directory. They are being used in the upcoming chapters and they refine the entire search into smaller steps:

• affhodge.g (this is a set of routines originally coded to compute affine Hodge numbers for this article.)
• preliminaries.g
• subdivide-four-simplex.g
• four-tropical-quintic-curves.g
• find-lines.g
• cleanup-and-plot.g

Basics of GAP

If you are not working with a terminal (e.g. when in Windows), instead of closing gap sessions and reopening with preloading a workspace, you should continue in the same session in what follows.

Subdividing the four-simplex

Once the gap prompt is available, enter this command in gap:

Read("subdivide-four-simplex.g");

Consequently, the code in the file subdivide-four-simplex.g will be executed. This first reads the file preliminaries.g which in turn reads affhodge.g and introduces a bunch of functions that will be needed later. The main calculation that is performed here is to subdivide the 5-fold multiple of the standard 4-simplex by the regular pattern that is depicted on the right of Figure 2.2 of page 12 in this article. The height function that realizes the subdivision is discussed in the article and it is given in the code by calling the function Height_KKMS from affhodge.g. An important point here is that we actually want to produce a small random perturbation of the height function in order to ensure to be in a generic situation which will later give the expected number of tropical lines when looking only at generic types of lines. The perturbation is realized by first rescaling and then randomly perturbing the KKMS height function, see the use of Random in the code. The perturbation doesn't change the subdivision in its combinatorial makeup but will affect the coordinates of the vertices of the tropical hypersurface that results from the height function. We like to choose as much of a generic position as possible while still being integral so that we can still use integral computations in what follows (you may say that we work with rational numbers with fixed denominator and actually cleared the denominator by rescaling everything). Once the height function is perturbed, we obtain the subdivision from dualizing the cone over the graph of the function, see the use of DualCone. The resulting object may be viewed as the tropical quintic hypersurface with respect to the perturbed height function. Finally, everything we did until here is being saved into the workspace file 5P3. The point of this step is to parallelize the further computation. So in the next paragraph, we begin a new gap session where the first step is to load this file of precomputed data. Obviously, if you want to use a different subdivision, i.e. combinatorially different tropical quintic, you want to edit the file subdivide-four-simplex.g accordingly by feeding it a different height function before its execution. You may exit gap now or you carry on in the same gap session and skip over the new start of gap in the coming section.

Prepare one of the five facets for the search

We have made a tropical quintic threefold in the previous section, now we are going to prepare the search for tropical lines in the toric degeneration associated with it. Start a new gap session with the stored workspace by the following command:

gap -L 5P3

This loads the previous computation. The 4-simplex has 5 facets and we expect 575 worth of lines in each facet. It is time to pick one of these facets, e.g. run the command

face_nr:=1;

to work with the first facet. Viable values are 1,2,3,4,5. Next run this command:

Read("four-tropical-quintic-curves.g");

This executes the code in the given file and it might take a bit. Gap spits out a warning about an unbound global variable which can safely be ignored. In the first paragraph of the file, the choice of facet from above enters in the way that we forget about most of the tropical quintic 3-fold in 4-space. We only consider its asymptotic part that runs our in the direction dual to the facet that we chose. At infinity in this direction, we find a tropical quintic surface in 3-space. This in turn has four asymptotic directions at each of which lies a tropical plane quintic curve. We are interested in determining these four plane quintics that lie in the four directions of the fan of P^3. In order to visualize the findings, we cut the tropical quintic surface with a large tetrahedron, so that each facet of the tetrahedron contains one of the four quintic curves. The variable projection_distance determines the size of this tetrahedron. It was already set in the code of the first section above. The second paragraph in the executed file is all about determining the four quintic curves and the remaining parts in the file are for its visualization. Three files are being produced, one in each of the last paragraphs:

• sage-command.sage
  A file that can be read in Sagemath via the command load("sage-command.sage") and then a subsequent executing of the command show(p,viewer='jmol') will show the picture below (if you have also Jmol installed, otherwise use a different viewer)
• data.g
  A file with the computed data in a form that can be read in gap via the command Read("data.g");
• current-P3
  The workspace file that we will resurrect in the next section.

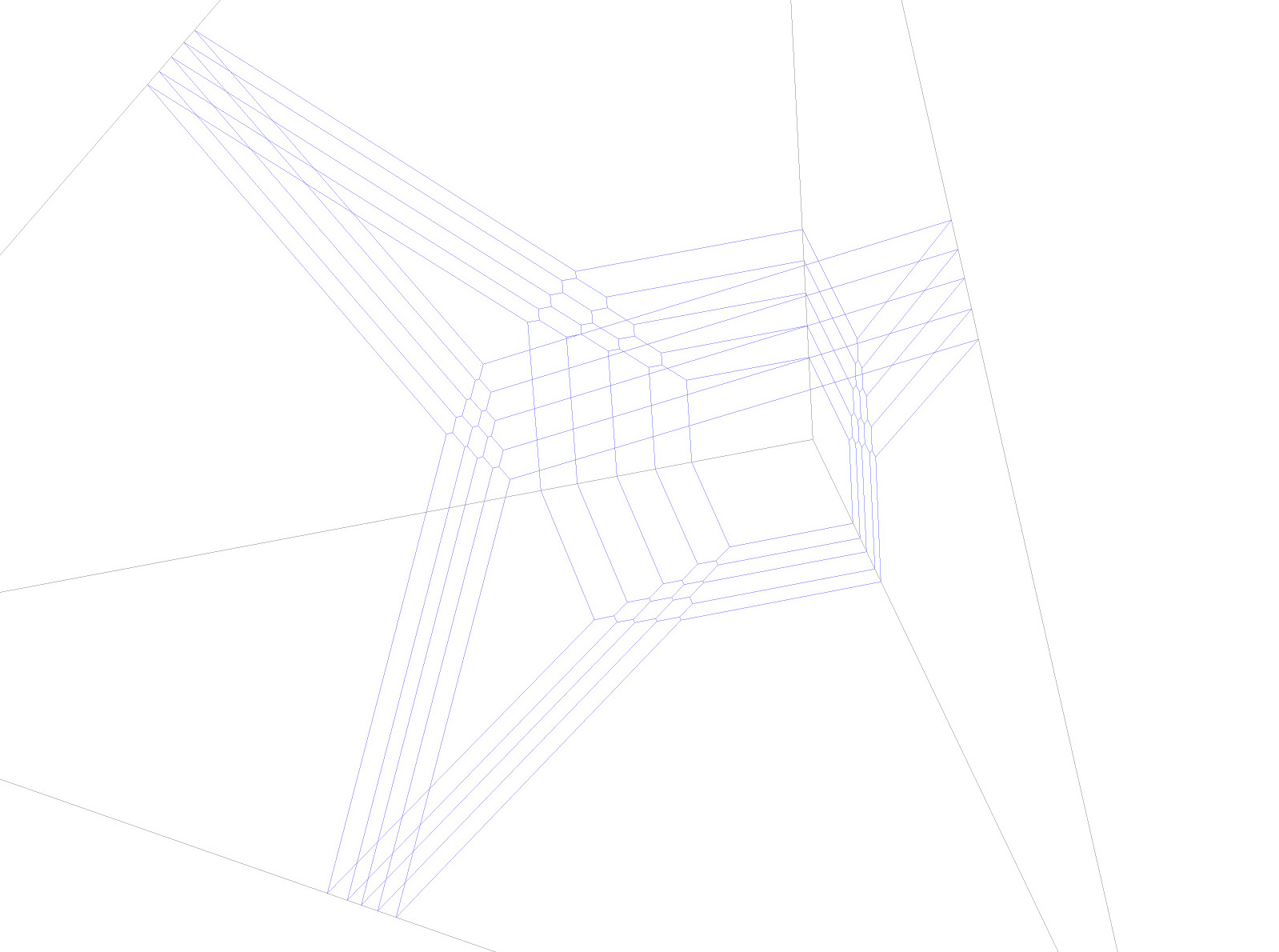
Search for the 575 worth of tropical lines meeting the four quintic curves

gap -L current-P3 -o 9999999999999999

where the -L part loads our previous computations and the -o part is to ensure enough memory is granted to the gap session. The search for the lines is executed by invoking

Read("find-lines.g");

though, as I said, before doing so, you might want to modify the first three lines of the file to something like

instance_nr:=1
interval_of_this_instance:=[((instance_nr-1)*3+1)..Minimum(((instance_nr-1)*3+3),45)];
#interval_of_this_instance:=[1..45];

That is, uncomment the second line and comment the third line in order to have the execution be only 1/15th of its total duration. By changing the assignment of instance_nr in the first line to a value between 1,..,15, you can run through the different parts of the search (and I used this for the parallelization). If you want the run to be even shorter, put interval_of_this_instance:=[1]; which would be 1/45th of the total duration and this might still take several hours. Modify the nested loops even further if you want a yet shorter snippet of the search.

The program will report on the screen whenever a tropical line has been found. It will write all lines found into the file lines.txt when it is done with the loop. The contents of this file can be read into gap by putting Read("lines.txt");

Now what is actually happening during the search? Each of the four tropical quintics has 45 edges (30 small ones and 15 long ones). We are cycling through a loop that looks at each of the 45^4 many combinations of picking one edge from each tropical quintic. For each such choice of four edges, we then check for the 3 different combinatorial types of a tropical line in 3-space, whether some translation and scaling of this combinatorial type could potentially hit all four selected edges from the tropical quintics. The combinatorial type tells us how to partition the 4 edges into 2+2, namely by which pair of edges is hit by tropical line legs that emanate from the same vertex. To check whether a tropical lines with the given data exists, we focus on one pair of quintic edges and take each edge times a real line in the the direction the wanted tropical curve leg and then we compute the intersection of these two copies of an embedded interval times a real line (point1 and point2 - and despite the name, this may be more or less than just a point). Only if the intersection is non-empty for both pairs of quintic edges, we carry on with the next check, namely whether the two resulting intersections can be joined by an interval in the of the central edge of the tropical line (which is uvec in the code). If there is a non-empty set of solutions, the result is appended to the list LINES and also the list MULT.

There is an additional check (in the code via if Intersection(Corners,comb)=[] then) for a situation that is not going to be recorded, namely we want to disregard tropical lines where the two (long) legs that emanate from a vertex meet a "corner pair" of edges of the tropical quintics. By a corner pair, we refer two a pair of edges that come from different quintic curves but the edges meet each other in a point. This point is necessarily on an edge of our "cut-off-tetrahedron" and the quintic edges must be among the 15 long edges for each quintic. We want to disregard tropical lines that meet a corner pair in this fashion because such a tropical line will not be rigid: it is possible to "slide" the vertex in a 1-dimensional family inside the plane spanned by the corner pair while still meeting all four quintic curves. Morally, such a tropical curve should correspond to an algebraic line that doesn't deform to the nearby smooth quintic as had been determined by Sheldon Katz, see the corresponding reference in "Tropically Constructed Lagrangians in Mirror Quintic Threefolds".

The "tropical lines" which result from the search as described above will not quite be what we want: we found too much stuff ! The following visualizations display stuff that we were not actually looking for but which will be part of the recorded data. The first is a situation of non-rigid lines, that is, a positive-dimensional family of lines. The plot shows these as surfaces rather than individual lines:

The second finding that we want to disregard is a line with length zero center edge. In other words, the combinatorial type of the line features only a single vertex. You see four such lines in the following plot:

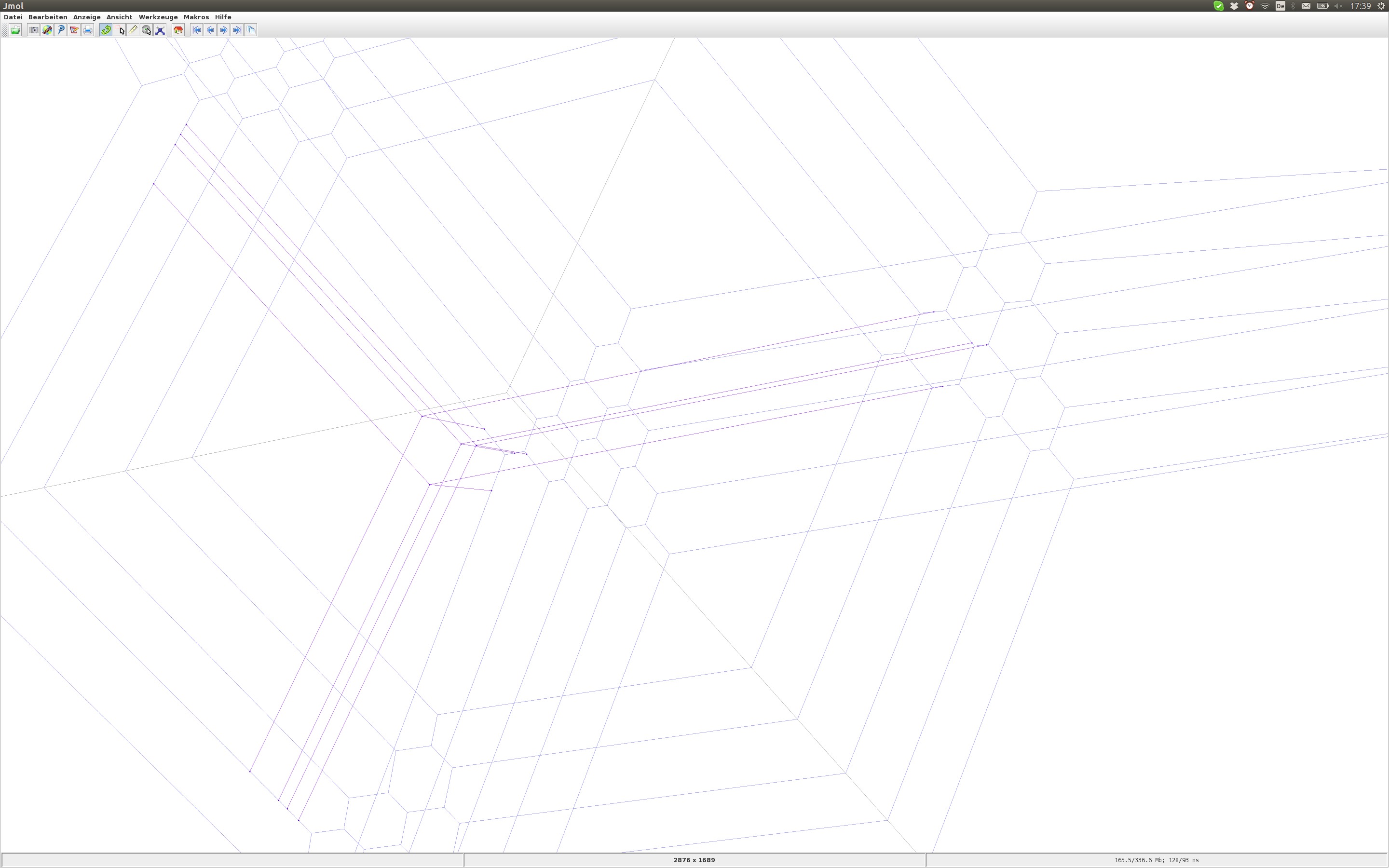
It is actually a bit of a puzzle to me why these two types of garbage appear. I had perturbed the KKMS height function generically and was hoping this would leave me with only rigid lines of generic type but this isn't so. Luckily, after removing the garbage, we end up with the expected number of lines when counting with multiplicity. It was known from the tropical cubic surface that too small embedding dimension or non-generic situations may yield too many tropical lines (infinite or more than expected finitely many), see "Anticanonical tropical cubic del Pezzos contain exactly 27 lines" and furthermore "Smooth tropical surfaces with infinitely many tropical lines" and "Tropical Lines on Cubic Surfaces". If we had not perturbed the KKMS height function, we would see even more special lines as the following plot demonstrates:

Garbage removal, final plot and the multiplicities

Start a new gap sesson simply with gap, no need to preload a prior session this time. Execute the command

Read("cleanup-and-plot.g");

This first reads the tropical quintics data from the file data.g. It then reads the file lines.txt that got saved after the search. The code then cycles through the lines and sorts the vertices of each edge and then also sorts the edges for each line. This is done so that it is possible to remove double findings of lines (an essential step for getting the right count). As explained in the previous section, we also remove positive-dimensional lines, degenerate lines and lines that meet a vertex of a quintic curve. What's leftover are only lines that are rigid and "generic". This yields the right count when counting with multiplicity. At the time of writing this and to my knowledge, there doesn't seem to exist a theorem that would predict this procedure yields the expected number, so what we do here is ad-hoc and empirical, yet it works. At the end of the cleaning (the first paragraph in the code), the list LINES contains the resulting lines and the list MULT contains the matching multiplicity data. The procedure that computes the multiplicity had been part of the file preliminaries.g and already got executed during the line search. The first entry of each item in the list MULT is the multiplicity of the corresponding line. The list lends records the end points of the tropical lines. Cheuk Yu Mak used this to compute which lines from different facets meet each other which led to the surprising finding that the incidence matrix has full rank, that is, the entire set of 2875 worth of tropical lines is connected.

The final paragraph in the executed file produces the file command-sage-final.sage which is for plotting the lines. In case this affects anyone else, I like to remark here that for the following to work in Sagemath, I weirdly had to execute make in the sage directory to first compile a bunch of extra things for sage before starting sage. In sage, we type the following three commands to display the lines with the viewer jmol:

sys.setrecursionlimit(10000)
load("command-sage-final.sage")
show(p,viewer='jmol')

Possibly after a little period of waiting, you should then be greeted with a rotatable view of the tropical lines, a snapshot of which might look as follows. Multiplicity 1 lines are violet, multiplicity 2 lines are red.

The 2875 worth of lines that the research article is based on

I finally provide here the files containing the result of the search that was done when writing the research article. It is important to know that for this setup projection_distance:=3000000 was used, different from the above and this is set in the file preliminaries.g. The number in the name of each of the following files corresponds to the number of the facet (as explained before):

• data1.g, lines1.txt
• data2.g, lines2.txt
• data3.g, lines3.txt
• data4.g, lines4.txt
• data5.g, lines5.txt

If you want to display the lines in lines1.txt, do the following: Modify preliminaries.g by setting the projection_distance to 3000000. Then modify cleanup-and-plot.g by replacing Read("lines.txt"); with Read("lines1.txt"); and also replace Read("data.g"); with Read("data1.g");. Then execute Read("cleanup-and-plot.g"); in gap and after that execute in sage the three commands for viewing given in the previous section.