
Effective Models for the QCD phase transition
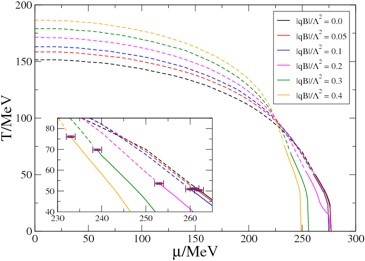
The phase diagram of the 2-flavour quark-meson model at finite temperature, chemical potential and external magnetic field B.
From [1].
Quantum ChromoDynamics is expected to be the correct theory for strong interactions, binding quarks inside protons, neutrons and pions. At low temperature and densities, the theory correctly predicts the confinement of colour charge, and the spontaneous breaking of chiral symmetry.
As temperature and/or density is increases, one or more phase transitions are expected to occur, whereby chiral symmetry is restored and colour-charged particles become deconfined. This has been confirmed at zero mu by lattice simulations, which are however very costly in terms of time and computer-power.
Based on “universality”, one would expect theories with the same global symmetries to have similar phase diagrams (in terms of the number of phases, whether the transition between adjoining phases is first, second or higher order). Much information can therefore be obtained through the study of much simpler scalar-fermion theories (Nambu-Jona-Lasinio, Linear sigma-model, non-linear sigma model, quark-meson model), either analytically in perturbation theory, or numerically through solving renormalization group flow equations [ERG].
Because the numerical effort is so much smaller that for full QCD, and because the introduction of a chemical potential does not suffer from the “sign” problem, this is currently the only reliable way to get information about the QCD phase diagram away from the zero density axis.
References (biased selection):
[1] Andersen, Tranberg: JHEP 1208 (2012) 002.
[2] Fukushima, Hatsuda: Rept. Prog. Phys. 74 (2011) 014001.
[3] Schaefer, Wambach: Nucl. Phys. A757 (2995) 479-491.
