
Quantum Fields in Curved Space-time
![Quantum field theory in flat Minkowski space is the basis of our extremely precise predictions within fundamental particle physics. It relies in part on the concept of renormalization, on symmetries among fundamental fields such as gauge invariance and the Lorentz symmetry of space-time [1].
Whereas in particle physics experiments, gravitational effects are completely negligible, in Cosmology they become crucial in the very early stages of the evolution of the Universe [2]. It now becomes important that the background geometry (through the metric tensor) is space and time dependent. This changes the dynamics of the fields, and also modifies the way we should approach renormalization.
A very important point is also that the fields are in principle never in complete thermal equilibrium, and so many processes such as inflation, reheating, baryogenesis must ultimately be treated as initial-value problems, and solved in real-time in terms of certain evolution equations.
In some cases, microscopic interactions are strong compared to the typical expansion time-scale of the Universe (the Hubble rate, H), and one may safely approximate the system of fields by thermal equilibrium. In other cases (typically during inflation) this is not an option.
********************************************************************************************************
In part because of the complexity of doing real-time evolution of quantum fields out of equilibrium, inflation model-building has traditionally been based on classical, homogeneous scalar fields (the inflaton, the curvaton), evolving in a non-trivial, Friedmann-Robertson-Walker background (encoded by the scale factor a(t)) under the influence of some field potential V. The equations of motion read:
These may in turn be simplified and solved analytically, through the use of the slow-roll approximation [3]. Alternatively, the equations may readily be solved numerically.
It is important to realize that what lies beneath this approach is that there exists a formulation of full quantum field theory in terms of the effective action, giving rise to time-evolution equations for the mean field (or one-point function), which in most cases is homogeneous. This is achieved through the computation of an effective potential V, which enters as above.
What is not obvious, is whether the Friedmann equation (2) also follows in terms of the effective V, since what actually enters is the variation of the effective action ww.r.t. the metric. In order for renormalization to go through, additional gravitational operators must be introduced, with corresponding counterterms [4], and it is for instance no longer clear that a useful slow-roll approximation exists.
**********************************************************************************************************
A further level of sophistication is reached when generalizing to the “2PI” formalism, where we introduce a new effective action in terms of the one- and two-point functions. Technically, solving the resulting evolution equations “resums” an infinite set of terms in the normal (1PI) effective action, a set which one for practical reasons would have to truncate in some way.
The numerical solution of these evolution equations (2PI, Relativistic Kadanoff-Baym, Real-time Schwinger-Dyson, Quantum Boltzmann) is very involved technically and in terms of computer time, and has only recently been implemented in expanding background [5]. Much work remains to be done in terms of renormalization and technical simplification [6].
References (biased selection):
[1] Peskin and Schroeder: “An Introduction to Quantum Field Theory”:Reading, USA: Addison-Wesley (1995) 842 p.
[2] Birrel and Davies: “Quantum Fields in Curved Space”, Cambridge Univ. Press, UK (1982) 340 p.
[3] Liddle and Lyth: “Cosmological Inflation and Large-Scale Structure”, Cambridge Univ. Press, UK (2000) 400 p.
[4] Markkanen, Tranberg: JCAP 1211 (2012) 027
[5] Tranberg: JHEP 0811 (2008) 037
[6] Serreau: Phys.Rev:Lett. 107 (2011) 191103; Serreau, Parentani: arXiv:1302.3262](QUantum_Fields_in_Curved_Space-time_files/shapeimage_2.png)










Particle number of an interacting scalar field in an FRW background, starting from an out-of-equilibrium state (black) and approaching equilibrium (blue).
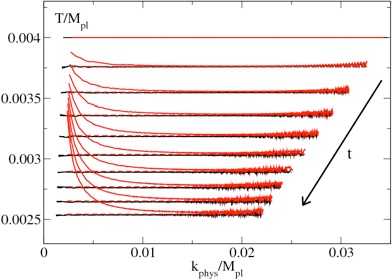
Particle spectrum of a scalar field in an FRW background. Initially in equilibrium (top red/black), all modes have the same effective temperature), the massive field (red) leaves equilibrium (black). On a finite grid, the k-range decreases through redshift, and eventually numerical noise interferes with the physics.
