MAXRD SYMBOL

SystematicAbsentQ

SystematicAbsentQ[group,{h,k,l}]
returns True if the hkl reflection is systematically absent for space group, and False otherwise.

SystematicAbsentQ[group,{{h1,k1,l1},{h2,k2,l2},…}]
returns a list where each reflection hkli has been checked for systematical absence for space group.

Details and OptionsDetails and Options

  • One may also enter the name of an entry in $CrystalData in group; the space group will be found automatically.
  • General extinction rules are applied, i.e. absences due to centring, screw axes or glide planes.
  • Options:
  • "Threshold"0declare the reflection 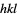extinct if 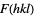is below this value (only checks if set to a number)

ExamplesExamplesopen allclose all

Basic Examples  (3)Basic Examples  (3)

Reflection is systematic absent (extinct) for space group :

In[1]:=
Click for copyable input
Out[1]=

while reflection is not:

In[2]:=
Click for copyable input
Out[2]=

In the case of silicon, reflection is not extinct, but is. This follows from the reflection condition for face-centred crystals (all Miller indices must be either odd or even).

In[1]:=
Click for copyable input
Out[1]=
In[2]:=
Click for copyable input
Out[2]=

Multiple reflections:

In[1]:=
Click for copyable input
Out[1]=
In[2]:=
Click for copyable input
Out[2]=

Scope  (1)Scope  (1)

Options  (1)Options  (1)

Applications  (1)Applications  (1)

Possible Issues  (2)Possible Issues  (2)

Mathematica code  (1)Mathematica code  (1)

Top