MAXRD SYMBOL
$SpaceGroups
$SpaceGroups
is an association containing data on the 230 crystallographic space groups.
DetailsDetails
- The Keys of $SpaceGroups are the plain string versions of the short Hermann–Mauguin. The Values are associations organised in the following structure:
-
Name Symbol (default symbol used in International Tables for Crystallography, volume A) Short Hermann–Mauguin symbol in string format Full Hermann–Mauguin symbol in string format Schoenflies symbol Hall symbol in string format Space group number Laue class Crystal system Properties Centrosymmetric? Sohncke group? Symmetry operations Special positions Multiplicity Wyckoff letter Site symmetry Coordinates - Many space groups have multiple representations (various cell choices, different permutations or choices of unique axis, etc.). This information is stored in an additional sub-association;
-
… Alternative settings Symbol of first alternative setting Name … Setting Origin shift (if applicable) Symmetry operations Special positions Symbol of second alternative setting … … - Under "Name", alternative symbols may appear, such as Fd-3m:2 which symbolises the space group
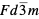 with the second origin choice.
with the second origin choice. - Not all alternative settings contain data on special positions; only those listed in the International Tables for Crystallograph, vol. A.
- The first sub-entry, "Symbol", in the "Name" entry is the formatted version of the symbol.
- The space groups numbered
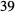 ,
, 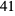 ,
, 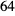 ,
, 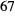 and
and 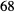 also have an "OldSymbol" entry that designates the symbol used with the old glide plane convention.
also have an "OldSymbol" entry that designates the symbol used with the old glide plane convention. - Hall symbols for the multiple cells of tetragonal, trigonal and hexagonal space groups are not found in the International Tables for Crystallography; this data has been collected from Grosse-Kunstleve's cctbx[2].
The HallString entries for multiple cells in the tetragonal space groups are based on the chosen directions a-b,a+b,c, while the alternative HallStringAlt is based on a+b,-a+b,c.
In the same manner, for the trigonal tiple cells the HallString is based on a-b,a+2b,c, while HallStringAlt2 corresponds to 2a+b,-a+b,c and HallStringAlt3 to a+2b,-2a-b,c.
Finally, for the hexagonal triple cells, HallString is based on a-b,a+2b,c; HallStringAlt2 on 2a+b,-a+b,c and HallStringAlt3 on a+2b,-2a-b,c. - The following space groups settings are not found in the International Tables for Crystallography, vol. A (even as unconventional cells):
-
1 P1 A1, B1, C1, F1, I1 2 P 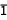
A 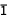 , B
, B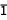 , C
, C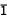 , F
, F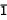 , I
, I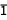
3 P2 B121, C112, A211 4 P21 B1211, C1121, A2111 5 C2 F121, F112, A211 6 Pm B1m1, C11m, Am11 7 Pc B1d1, B1a1, C11a, C11d, Ad11, Ab11 8 Cm F1m1, F11m, Fm11 9 Cc F1d1, F11d, Fd11 10 P2/m B12/m1, C112/m, A2/m11 11 P21/m B121/m1, C1121/m, A21/m11 12 C2/m F12/m1, F112/m, F2/m11 13 P2/c B12/d1, B12/a1, C112/d, C112/a, A2/b11, A2/d11 14 P21/c B121/d1, B121/a1, C1121/d, A21/b11, A21/d11 15 C2/c F12/d1, F112/d, F2/d11 75–142 (tetragonal) PC and IF 143–165 (hexagonal lattice) H centring - The properties "CentrosymmetricQ" and "SohnckeGroupQ" have Boolean values. Centric is synonymous with centrosymmetric in this sense, and a space group that is a Sohncke group can also be said to be chiral.
- $SpaceGroups is loaded from:
Related LinksRelated Links
- [1] T. Hahn, Space-Group Symmetry, 5th ed., International Tables for Crystallography. Kluwer Academic Publishers, 2002, volume A. Website: http://it.iucr.org/A/.
- [2] R.W. Grosse-Kunstleve, cctbx - Multiple cell C or F and triple cell H settings, Oct. 2001. [Online]. https://cci.lbl.gov/cctbx/multiple_cell.html (accessed 2017–11–28).

